Mathematics, to put it simply, is the study of numbers. But it is not merely numbers. Mathematics also involves structure, space, and change. Mathematics can be studied as its own discipline or can be applied to other field of studies.
Applied mathematics is those which are used in other sciences such as engineering, physics, chemistry, medicine, even social sciences, etc. Pure mathematics on the other hand is the theoretical study of the subject, and practical applications are discovered through its study.
26 Types of Math
The word mathematics was coined by the Pythagoreans in the 6th century from the Greek word μάθημα (mathema), which means “subject of instruction.” There are many different types of mathematics based on their focus of study. Here are some of them:
1. Algebra
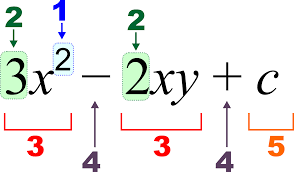
Algebra is a broad division of mathematics. Algebra uses variable (letters) and other mathematical symbols to represent numbers in equations. It is basically completing and balancing the parts on the two sides of the equation.
It can be considered as the unifying type of all the fields in mathematics. Algebra’s concept first appeared in an Arabic book which has a title that roughly translates to ‘the science of restoring of what is missing and equating like with like.’ The word came from Arabic which means completion of missing parts.
See Also: 7 Types of Fractions
2. Geometry
The word geometry comes from the Greek words ‘gē’ meaning ‘Earth’ and ‘metria’ meaning ‘measure’. It is the mathematics concerned with questions of shape, size, positions, and properties of space.
It also studies the relationship and properties of set of points. It involves the lines, angles, shapes, and spaces formed.
3. Trigonometry
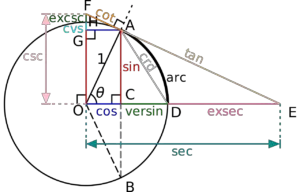
Trigonometry comes from the Greek words ‘trigōnon’ which means ‘triangle’ and ‘metria’ which means ‘measure’. As its name suggests, it is the study the sides and angles, and their relationship in triangles.
Some real life applications of trigonometry are navigation, astronomy, oceanography, and architecture.
4. Calculus
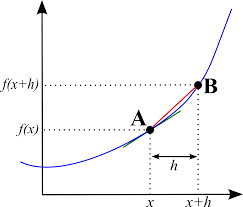
Calculus is an advanced branch of mathematics concerned in finding and properties of derivatives and integrals of functions. It is the study of rates of change and deals with finding lengths, areas, and volumes.
Calculus is used by engineers, economists, scientists such as space scientists, etc.
5. Linear Algebra
Linear algebra is a branch of mathematics and a subfield of algebra. It studies lines, planes, and subspaces. It is concerned with vector spaces and linear mappings between those spaces.
This branch of mathematics is used in chemistry, cryptography, geometry, linear programming, sociology, the Fibonacci numbers, etc.
6. Combinatorics

The name combinatorics might sound complicated, but combinatorics is just different methods of counting. The word was derived from the word ‘combination’, therefore it is used to combine objects following rules of arranging those objects.
There are two combinatorics categories: enumeration and graph theory. Permutation, an arrangement where order matters, is often used in both of the categories.
7. Differential Equations
As the name suggest, differential equations are not really a branch of mathematics, rather a type of equation. It is any equation that contains either ordinary derivatives or partial derivatives.
The equations define the relationship between the function, which represents physical quantities, and the derivatives, which represents the rates of change.
8. Real Analysis
Real analysis is also called the theory of functions of a real variable. It is concerned with the axioms dealing with real numbers and real-valued functions of a real-variable.
It is pure mathematics, and is good for people who like plane geometry and proving.
9. Complex Analysis

Complex analysis is also called the theory of functions of a complex variable. It deals with complex numbers and their derivatives, manipulation, and other properties. Complex analysis is applied in electrical engineering, when launching satellite, etc.
10. Abstract Algebra
Sometimes called modern algebra, abstract algebra is an advanced field in algebra concerning the extension of algebraic concepts such as real number systems, complex numbers, matrices, and vector spaces.
One application of abstract algebra is cryptography; elliptic curve cryptography involves a lot of algebraic number theory and the likes.
11. Topology

Topology is a type of geometry developed in the 19th century. Its name’s Greek origin, which is ‘topos’, means place. Unlike the other types of geometry, it is not concerned with the exact dimensions, shapes, and sizes of a region.
It studies the physical space a surface unaffected by distortion contiguity, order, and position. Topology is applied in the study of the structure of the universe and in designing robots.
12. Number Theory

Number theory, or higher arithmetic, is the study of positive integers, their relationships, and properties. It is sometimes referred to as “The Queen of Mathematics” because of its foundational function in the subject.
13. Logic

Logic is the discipline in mathematics that studies formal languages, formal reasoning, the nature of mathematical proof, probability of mathematical statements, computability, and other aspects of the foundations of mathematics.
It aims to eliminate any confusion that can be caused by the vagueness of the natural language.
See Also: 12 Different Types of Watch Bezels
14. Probability
Probability is the branch of mathematics calculating the chances of some things to take place based on the number of the possible cases to the whole number of cases possible. Numbers from 0-1 are used to express the chances of something to occur.
0 means it can never happen and 1 means it will always happen. Real-life applications are in gambling, lottery, sports analysis, games, weather forecasting, etc. Even the chance of an earthquake or a volcano erupting are given a probability.
Read Also: Different Types of Magma
15. Statistics

Statistics are the collection, analysis, measurement, interpretation, presentation and summarization of data. Statistics is used in many fields such as business analytics, demography, epidemiology, population ecology, etc.
16. Game Theory
Game theory is a branch of mathematics which also involves psychology, economics, contract theory, and sociology. It analyses strategies for dealing with competitive strategies where the outcome also depends on other actions of other partaker in the activity.
It is applied in business, wars, political sciences, biology, philosophy, etc.
17. Functional Analysis

Functional analysis is under the field of mathematical analysis. Its foundation is the study of vector spaces that has limit-related structure such as topology, inner product, norm, etc.
It was developed through the study of functions and the formulation of properties of transformation. Functional analysis is found to be useful for differential and integral equations.
18. Algebraic Geometry
Algebraic geometry is a branch of mathematics that uses algebraic expressions to describe geometric properties of structures.
19. Differential Geometry
Differential geometry is a field in mathematics that utilizes different mathematical techniques (differential calculus, integral calculus, linear algebra, and multilinear algebra) to study geometric problems.
It is used in different studies of electromagnetism, econometrics, geometric modeling, digital signal processing in engineering, study of geological structures.
20. Dynamical Systems (Chaos Theory)
Dynamical Systems (also referred to as chaos theory) is a mathematical concept where the relationship of a point in space to time is described a fixed set of rules. This concept explains the swinging of a clock pendulum, flow of water in a pipe, number of fish in a lake during springtime, etc.
21. Numerical Analysis
Numerical analysis is an area in mathematics which develops, evaluates, and applies algorithms for numerically solving problems that occur throughout the natural sciences, social sciences, medicine, engineering and business.
22. Set Theory
Set theory is a discipline in mathematics that is concerned with the formal properties of a well-defined set of objects as units (regardless of the nature of each element) and using set as a means of expression of other branch of math.
Every object in the set has something similar or follows a rule, and they are called the elements.
23. Category Theory
Category theory is a formalism that is used for representing and manipulating concepts and symbolic representations of domains. Here, the collection of objects and of arrows formalizes mathematical structure.
24. Model Theory
Model theory in mathematics is the study of different structures from a logical standpoint. It involves interpretation of formal and natural languages and the kinds of classifications they can make.
25. Mathematical Physics
Mathematics as mentioned earlier is used in many different other fields. Physics is just one of them. Mathematical physics refers to the mathematical methods applied for different studies and development in physics.
26. Discrete Mathematics
Unlike the many other ones mentioned above, discrete mathematics is not a branch, but a description of the study of mathematical structures that are discrete rather than continuous.
Discrete objects, in simple languages, are the countable objects such as integers. Therefore, discrete mathematics does not include calculus and analysis.


please more about algebra, trigonometry and calculus
I have a question. A teacher of mine discussed a class she took in college converting language into mathematics. She mentioned the name of the class, but I suffer from TBI and forget details. I remember her saying all of language is mathematics and not just the operative words. I would like to read up on that.
Could be logic.
What about quantum mathematics?
i’m going for set theory
If you think about it, in language there are nouns and adjectives to describe things and algebra, topology, set theory, describe things. There are also verbs and adjectives to describe actions and that’s more like calculus and analysis. So, yeah, language is lime mathematics except np ore general, less precise . My BA degree was in English but after graduating I went back to school a few years later and studied undergraduate and graduate level mathematics but then life got in the way and I never finished graduate school. But I love both mathematics and language and have always thought about of them as quite similar. I spent most of my working life as a computer programmer and now that I’m retired I still spent at least part of every day messing about with math.
In Section 6, you use the word “in” instead of “it”:
therefore in is used to combine objects following rules of arranging those objects.
Good catch, thanks.
You missed Laplace Transforms. Isn’t that another another type of math?
Thank you for the brief descriptions of 26 types of math. I am a writer currently dealing with a character (Jaz the Jenius)
to whom I previously awarded “6 upper-level degrees”. It occurred to me that I should probably know at least the names of the types of math in which he specialized.